Piero della Francesca e l'importanza del suo trattato “De quinque corporibus regularibus”

27

È risaputo che Piero della Francesca sia stato, oltre che un eccezionale artista, anche un trattatista di alto livello. Chiunque abbia studiato anche un minimo di storia dell’arte del Rinascimento, ha sempre saputo che il grande artista toscano scrisse quattro trattati, tra i quali il fondamentale De prospectiva pingendi, dedicato alla prospettiva scientifica. Talmente fondamentale, che quando si parla dei trattati di Piero, si rischia di snobbare gli altri, e in particolare il De quinque corporibus regolaribus, di importanza non inferiore a quella dello scritto pierfrancescano più famoso. E infatti sono pochi i libri di storia dell’arte che forniscono informazioni approfondite su questo trattato: ci si limita, il più delle volte, a sottolineare che è un libro sui cinque solidi regolari, e poi si passa oltre.

Tuttavia, una domanda nasce spontanea: perché Piero della Francesca avrebbe dovuto dedicare un intero trattato a un argomento così tecnico e specifico come quello dei cinque solidi regolari? Partiamo da una premessa. Com’è noto, Piero della Francesca fu uno degli artisti più attratti dalle leggi matematiche e geometriche che regolano lo spazio, in quanto ritenute da lui (come da altri artisti) fondamentali per risolvere una delle più annose questioni della pittura: la rappresentazione di uno spazio tridimensionale su un supporto bidimensionale. Per questo motivo, secondo Piero della Francesca ogni studio che riguarda la geometria è dotato di un fine pratico di elevata importanza: riuscire a riprodurre lo spazio della realtà su un muro o su una tavola (Piero non lavorò mai sulla tela). Però, prima di andare oltre, vediamo più da vicino di cosa tratta il De quinque corporibus regularibus.

Due fogli del De quinque corporibus regularibus (Manoscritto cod. Urb. lat. 632 fol. 40 verso - 41 recto; Roma, Città del Vaticano, Biblioteca Apostolica Vaticana. Il manoscritto è di autore sconosciuto, le correzioni e le note sono di Piero della Francesca)

Abbiamo detto che il trattato, scritto in latino, è interamente dedicato ai cinque solidi regolari. Questi ultimi altro non sono che poliedri, ovvero solidi la cui superficie è formata da facce poligonali, che rispetto a tutti gli altri poliedri hanno la caratteristica di avere tutte le facce, gli spigoli e gli angoli uguali, di uguale misura. La scoperta dei solidi regolari è attribuita a Pitagora, ma il primo che ne parla è Platone nel suo Timeo: Platone fu il primo a descriverli in modo particolareggiato, anche se il primo a descrivere come si costruiscono sarà, qualche decennio dopo, Euclide (e infatti Piero si ispirò proprio a Euclide). Tuttavia, Platone non si limitò solo a descriverli, perché si preoccupò anche di conferire ai solidi regolari una valenza simbolica: quattro di loro erano dunque associati ai quattro elementi dell’universo, e uno (il dodecaedro) era simbolo dell’universo stesso. A Piero tutto questo non interessava: Piero della Francesca studiò i cinque poliedri regolari per puro fine pratico. Ma quali sono i cinque poliedri regolari? Eccoli: la piramide a base triangolare, vale a dire il tetraedro (quattro facce triangolari, ovviamente parliamo di triangoli equilateri), il cubo detto anche esaedro (sei facce quadrate), l’ottaedro (otto facce triangolari), il dodecaedro (dodici facce pentagonali) e l’icosaedro (venti facce triangolari). Non sono possibili altri solidi regolari, cioè non è possibile trovare altre combinazioni che diano come risultato un poliedro che abbia tutte le facce di pari superficie (e che soprattutto siano poligoni regolari), tutti gli spigoli di egual misura, e tutti gli angoli della stessa apertura.

Uno dei migliori amici di Piero della Francesca, il matematico Luca Pacioli, sviluppò nel suo trattato De divina proportione quanto scritto dal pittore, e si fece illustrare il suo trattato da Leonardo da Vinci. Ecco come Leonardo raffigurò i poliedri regolari:

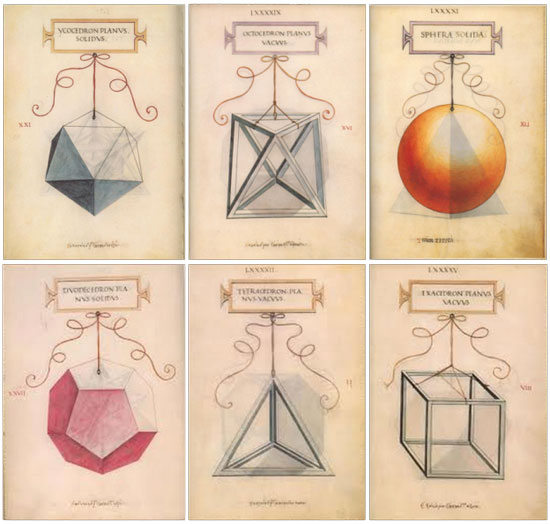I cinque poliedri regolari (assieme alla sfera, nella quale tutti possono essere inscritti) disegnati da Leonardo da Vinci per il De divina proportione di Luca Pacioli nel 1509. In alto, da sinistra: icosaedro, ottaedro, sfera. In basso, da sinistra: dodecaedro, tetraedro, cubo o esaedro.

Ma veniamo all’importanza dell’opera, e al motivo per cui Piero della Francesca la scrisse. L’artista era consapevole che esisteva un profondo legame tra i cinque corpi regolari e la prospettiva, la tecnica che, come si è detto, permette la raffigurazione dello spazio tridimensionale su un supporto bidimensionale. Esercitarsi sui solidi regolari voleva dire intanto imparare il disegno prospettico, fondamentale per una rappresentazione dello spazio su base scientifica: e infatti, il libro è pieno di esercizi matematici e geometrici, alcuni dei quali anche piuttosto astratti, che aiutano l’artista che lo legge a far pratica di disegno, a imparare a conoscere lo spazio. Rappresentare uno spazio tridimensionale, per Piero, presuppone che gli oggetti che lo compongono vengano studiati in modo analitico, nelle loro forme, nella loro posizione rispetto al luogo che li contiene, nel loro rapporto con gli altri oggetti. Lo studio dei poliedri regolari non è che un modo per approcciarsi a quello che sarà, poi, lo studio di forme più complesse (come la figura umana, probabilmente la più complicata da rappresentare in prospettiva).

Il fatto che ci sia un legame tra disegno prospettico e disegno dei solidi geometrici ci viene rivelato anche da un particolare estraneo alla trattazione in sé, ma comunque significativo: il libello De quinque corporibus regularibus che, non lo abbiamo ancora detto, fu scritto tra il 1482 e il 1492, è dedicato al terzo duca d’Urbino, Guidobaldo da Montefeltro. Il precedente De prospectiva pingendi, composto all’incirca tra il 1472 e il 1475, era invece dedicato al padre di Guidobaldo, Federico da Montefeltro: c’è insomma una continuità tra il trattato più antico e quello più recente, quindi c’è una continuità tra gli argomenti affrontati, e questa continuità è ben esemplificata dalle dediche. Ma non solo: è Piero stesso, nella dedica, a mettere in rapporto il De quinque corporibus regularibus con il De prospectiva. Leggiamo, infatti, queste parole: “Nec dedignabitur celsitudo tua ex hoc iam emerito, et fere vetustate consumpto agello, unde et illustrissimus genitor tuus, uberiores percepit, hos exiles et inanes fructus suscipere, et libellum ipsum inter innumera amplissimae tuae, paternaeque bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, prò pedissequo et aliorum servulo, vel in angulo collocare”. Che tradotte suonano più o meno così: “Vostra Altezza non disdegnerà di accettare, da questo campicello ormai consumato dalla vecchiezza, e da cui il Vostro illustrissimo genitore già raccolse più ricchi frutti, questo magro e vano prodotto, né disdegnerà di collocare questo libretto, tra gli innumerevoli volumi della Vostra vastissima biblioteca paterna, in un angolo vicino al mio opuscolo sulla Prospettiva, che scrissi negli anni passati come piccolo servo fedele”.

Sezione IV (“I corpi geometrici”) della mostra Piero della Francesca. Il disegno tra arte e scienza, Reggio Emilia, Palazzo Magnani, 14 marzo - 14 giugno 2015. La foto è di Mostre-rò che ringraziamo per la gentile concessione!

Nella dedica del libro sui solidi regolari, viene anche brevemente esposto il contenuto del trattato. Lo scritto si compone, infatti, di quattro parti: la prima contiene problemi di geometria piana, importanti perché senza nozioni di geometria piana non si può studiare la geometria dei solidi. Quest’ultima viene trattata nelle parti successive: la seconda introduce i poliedri regolari e propone esercizi su questo tema, nella terza si parla dei poliedri inscritti in altri poliedri e infine l’ultima parte è dedicata ai poliedri irregolari. Ogni esercizio è corredato di disegni esplicativi: una pratica che oggi ci pare scontata, ma a quei tempi non era così. Per esempio, Leon Battista Alberti, che nel suo De pictura esponeva diversi principi della geometria euclidea (Euclide fu un punto di riferimento importante sia per Alberti che per Piero), non aveva aggiunto alcun disegno, dato che presso gli intellettuali umanisti dell’epoca era diffusa la convinzione che le parole fossero di per sé sufficienti a spiegare un concetto. Piero della Francesca invece, da individuo pragmatico e concreto quale era, si accorse che per far arrivare meglio i concetti è necessario aiutarsi con i disegni, che non mancano mai nei suoi trattati.

Concludiamo dicendo che per Piero i solidi regolari non erano solo degli oggetti su cui esercitarsi. Spesso, il pittore utilizzava i poliedri regolari per costruire lo spazio all’interno del quale ambientava i dipinti. Abbiamo quindi analizzato due sue celebri opere, la Madonna del Parto e la Flagellazione, per cercare strutture spaziali derivanti dai solidi regolari. Si può quindi notare come la Madonna del Parto sia stata realizzata a partire da un dodecaedro, mentre l’ambientazione in cui Gesù subisce la flagellazione nel famoso dipinto urbinate, è nient’altro che un cubo aperto e studiato in prospettiva. Ma siamo convinti che anche in altri dipinti di Piero si possa fare lo stesso tipo di indagine... !

Piero della Francesca, Madonna del parto (1455 circa; Monterchi, Museo della Madonna del Parto) nello spazio segnato da un dodecaedro. Sia in questa immagine che nella successiva abbiamo schiarito i colori dei dipinti per rendere più evidenti la forme geometriche.

Piero della Francesca, Flagellazione (1460 circa; Urbino, Galleria Nazionale delle Marche) con evidenziate le linee della prospettiva, il punto di fuga (il pallino rosso) e le linee del cubo entro cui è ambientata la scena di sinistra.

L'autore di questo articolo: Federico Giannini

Nato a Massa nel 1986, si è laureato nel 2010 in Informatica Umanistica all’Università di Pisa. Nel 2009 ha iniziato a lavorare nel settore della comunicazione su web, con particolare riferimento alla comunicazione per i beni culturali. È giornalista iscritto all’Ordine dal 2017, specializzato in arte e storia dell’arte. Nel 2017 ha fondato con Ilaria Baratta la rivista Finestre sull’Arte, iscritta al registro della stampa del Tribunale di Massa dal giugno 2017. Dalla fondazione è direttore responsabile della rivista. Collabora e ha collaborato con diverse riviste, tra cui Art e Dossier e Left, e per la televisione è stato autore del documentario Le mani dell’arte (Rai 5) ed è stato tra i presentatori del programma Dorian – L’arte non invecchia (Rai 5). Ha esperienza come docente per la formazione professionale continua dell’Ordine e ha partecipato come relatore e moderatore su temi di arte e cultura a numerosi convegni (tra gli altri: Lu.Bec. Lucca Beni Culturali, Ro.Me Exhibition, Con-Vivere Festival, TTG Travel Experience).

Lo spettacolare “Convito in casa di Levi” (o del fariseo) degli Haeredes Pauli a Verona

Il “pulpito meraviglioso” di Donatello e Michelozzo per il Duomo di Prato

C'è un nuovo dipinto di Lorenzo Lotto a Recanati? La “provocazione” della grande mostra di Macerata

Il fondotinta della Gioconda e il mascara della Vecchia di Giorgione

La volta della Stanza dell'Incendio di Borgo. Una nota storica importante

Nella Svizzera del Cinquecento si andava alle terme: ecco com'erano le spa del XVI secolo