Piero della Francesca et l'importance de son traité "De quinque corporibus regularibus".

Il est bien connu que Piero della Francesca n’était pas seulement un artiste exceptionnel, mais aussi un auteur de traités très accompli. Quiconque a étudié un tant soit peu l’histoire de l’art de la Renaissance a toujours su que le grand artiste toscan avait écrit quatre traités, dont le fondamental De prospectiva pingendi, consacré à la perspective scientifique. Tellement fondamental qu’en parlant des traités de Piero, on risque de snober les autres, et en particulier le De quinque corporibus regolaribus, non moins important que le plus célèbre des écrits de Piero. Et de fait, rares sont les livres d’histoire de l’art qui fournissent des informations approfondies sur ce traité: la plupart du temps, on se contente de rappeler qu’il s’agit d’un livre sur les cinq solides réguliers, et l’on passe à autre chose.

Cependant, une question se pose spontanément: pourquoi Piero della Francesca aurait-il consacré un traité entier à un sujet aussi technique et spécifique que les cinq solides réguliers? Commençons par une prémisse. Comme on le sait, Piero della Francesca a été l’un des artistes les plus attirés par les lois mathématiques et géométriques qui régissent l’espace, car il les considérait (comme d’autres artistes) comme fondamentales pour résoudre l’un des problèmes les plus anciens de la peinture: la représentation d’un espace tridimensionnel sur un support bidimensionnel. C’est pourquoi, selon Piero della Francesca, toute étude concernant la géométrie est dotée d’un objectif pratique très important: pouvoir reproduire l’espace de la réalité sur un mur ou un panneau (Piero n’a jamais travaillé sur toile). Mais avant d’aller plus loin, regardons de plus près ce qu’est le De quinque corporibus regularibus.

Deux folios du De quinque corporibus regularibus (Manuscrit cod. Urb. lat. 632 fol. 40 verso - 41 recto ; Rome, Cité du Vatican, Bibliothèque du Vatican. Le manuscrit est d’un auteur inconnu, les corrections et les notes sont de Piero della Francesca)

Nous avons dit que le traité, écrit en latin, est entièrement consacré aux cinq solides réguliers. Ces derniers ne sont rien d’autre que des polyèdres, c’est-à-dire des solides dont la surface est formée de faces polygonales qui, par rapport à tous les autres polyèdres, ont la particularité d’avoir toutes leurs faces, arêtes et angles égaux, de même taille. La découverte des solides réguliers est attribuée à Pythagore, mais le premier à en parler est Platon dans son Timée: Platon est le premier à les décrire en détail, même si le premier à décrire leur construction sera, quelques décennies plus tard, Euclide (et Piero s’est d’ailleurs inspiré d’Euclide). Mais Platon ne s’est pas contenté de les décrire, il a également pris soin de donner aux solides réguliers une valeur symbolique: quatre d’entre eux étaient ainsi associés aux quatre éléments de l’univers, et l’un d’eux (le dodécaèdre) était un symbole de l’univers lui-même. Tout cela n’intéressait pas Piero: Piero della Francesca étudiait les cinq polyèdres réguliers dans un but purement pratique. Mais quels sont les cinq polyèdres réguliers? Les voici: la pyramide à base triangulaire, c’est-à-dire le tétraèdre (quatre faces triangulaires, il s’agit évidemment de triangles équilatéraux), le cube appelé aussi hexaèdre (six faces carrées), l’octaèdre (huit faces triangulaires), le dodécaèdre (douze faces pentagonales) et l’icosaèdre (vingt faces triangulaires). Aucun autre solide régulier n’est possible, c’est-à-dire qu’il n’est pas possible de trouver d’autres combinaisons permettant d’obtenir un polyèdre dont toutes les faces ont la même surface (et sont avant tout des polygones réguliers), dont toutes les arêtes ont la même taille et dont tous les angles ont la même ouverture.

L’un des meilleurs amis de Piero della Francesca, le mathématicien Luca Pacioli, a développé ce que le peintre avait écrit dans son traité De divina proportione et l’a fait illustrer par Léonard de Vinci. Voici comment Léonard a représenté les polyèdres réguliers :

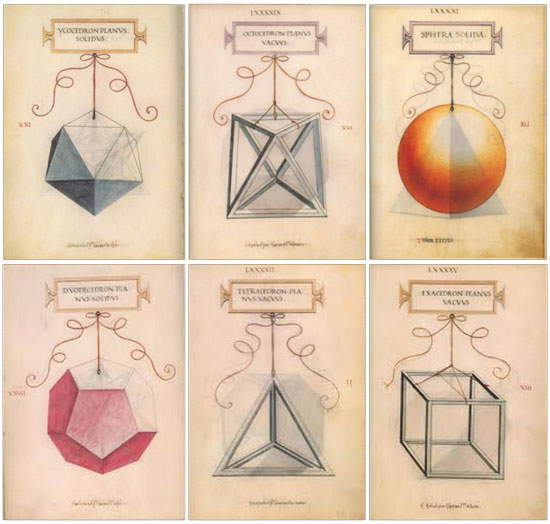Les cinq polyèdres réguliers (ainsi que la sphère, dans laquelle ils peuvent tous être inscrits) dessinés par Léonard de Vinci pour le De divina proportione de Luca Pacioli en 1509. En haut, de gauche à droite: icosaèdre, octaèdre, sphère. En bas, à partir de la gauche: dodécaèdre, tétraèdre, cube ou hexaèdre.

Mais venons-en à l’importance de l’œuvre et à la raison pour laquelle Piero della Francesca l’a écrite. L’artiste était conscient qu’il existait un lien profond entre les cinq corps réguliers et la perspective, la technique qui, comme nous l’avons vu plus haut, permet de représenter un espace tridimensionnel sur un support bidimensionnel. Pratiquer les solides réguliers signifiait en même temps apprendre le dessin en perspective, qui est fondamental pour une représentation de l’espace sur une base scientifique: et en effet, le livre est plein d’exercices mathématiques et géométriques, certains d’entre eux très abstraits, qui aident l’artiste qui le lit à pratiquer le dessin, à apprendre à connaître l’espace. Représenter un espace tridimensionnel, pour Piero, suppose que les objets qui le composent soient étudiés de manière analytique, dans leurs formes, dans leur position par rapport au lieu qui les contient, dans leur relation avec d’autres objets. L’étude des polyèdres réguliers n’est qu’une façon d’aborder ce qui sera plus tard l’étude de formes plus complexes (comme la figure humaine, probablement la plus compliquée à représenter en perspective).

Le fait qu’il existe un lien entre le dessin en perspective et le dessin des solides géométriques nous est également révélé par un détail étranger au traité lui-même, mais néanmoins significatif: l’opuscule De quinque corporibus regularibus qui, nous ne l’avons pas encore mentionné, a été écrit entre 1482 et 1492, est dédié au troisième duc d’Urbino, Guidobaldo da Montefeltro. Le précédent De prospectiva pingendi, composé approximativement entre 1472 et 1475, était quant à lui dédié au père de Guidobaldo, Federico da Montefeltro: il y a donc une continuité entre le traité le plus ancien et le plus récent, donc une continuité entre les sujets abordés, et cette continuité est bien illustrée par les dédicaces. Mais pas seulement: c’est Piero lui-même, dans la dédicace, qui met en relation le De quinque corporibus regularibus avec le De prospectiva. Nous lisons en effet ces mots: “Nec dedignabitur celsitudo tua ex hoc iam emerito, et fere vetustate consumpto agello, unde et illustrissimus genitor tuus, uberiores percepit, hos exiles et inanes fructus suscipere, et libellum ipsum inter innumera amplissimae tuae, paternaeque bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, prò pedissequo et aliorum servulo, vel in angulo collocare”. Ce qui se traduit à peu près ainsi: “Votre Altesse ne dédaignera pas d’accepter, de ce champ maintenant consumé par la vieillesse, et dont votre illustre parent a déjà récolté de plus riches fruits, ce maigre et vain produit, ni de placer cet opuscule, parmi les innombrables volumes de votre vaste bibliothèque paternelle, dans un coin à côté de mon opuscule sur la Perspective, que j’ai écrit dans les années passées en tant que fidèle petit serviteur”.

Section IV (“Les corps géométriques”) de l’exposition Piero della Francesca. Il disegno tra arte e scienza, Reggio Emilia, Palazzo Magnani, 14 mars - 14 juin 2015. La photo est de Mostre-rò, que nous remercions pour son aimable autorisation !

Dans la dédicace du livre sur les solides réguliers, le contenu du traité est également brièvement exposé. En fait, le document se compose de quatre parties: la première contient des problèmes de géométrie plane, qui sont importants car sans notions de géométrie plane, on ne peut pas étudier la géométrie des solides. Cette dernière est traitée dans les parties suivantes: la deuxième introduit les polyèdres réguliers et propose des exercices sur ce sujet, la troisième traite des polyèdres inscrits dans d’autres polyèdres et enfin la dernière partie est consacrée aux polyèdres irréguliers. Chaque exercice est accompagné de dessins explicatifs: une pratique qui nous semble évidente aujourd’hui, mais qui ne l’était pas à l’époque. Par exemple, Leon Battista Alberti, qui a exposé plusieurs principes de la géométrie euclidienne dans son De pictura(Euclide était une référence importante tant pour Alberti que pour Piero), n’a pas ajouté de dessins, car les intellectuels humanistes de l’époque pensaient que les mots suffisaient à expliquer un concept. Piero della Francesca, en revanche, en homme pragmatique et concret qu’il était, a compris que pour mieux faire passer les concepts, il fallait s’aider de dessins, qui n’ont jamais manqué dans ses traités.

Concluons en disant que pour Piero, les solides réguliers n’étaient pas seulement des objets sur lesquels s’exercer. Souvent, le peintre utilisait des polyèdres réguliers pour construire l’espace dans lequel il plaçait ses tableaux. Nous avons donc analysé deux de ses œuvres célèbres, la Madonna del Parto et la Flagellation, à la recherche de structures spatiales dérivées des solides réguliers. Nous voyons ainsi que la Madonna del Parto a été créée à partir d’un dodécaèdre, tandis que le cadre dans lequel Jésus subit la flagellation dans le célèbre tableau d’Urbino n’est rien d’autre qu’un cube ouvert étudié en perspective. Mais nous sommes convaincus que le même type de recherche peut être effectué dans d’autres tableaux de Piero... !

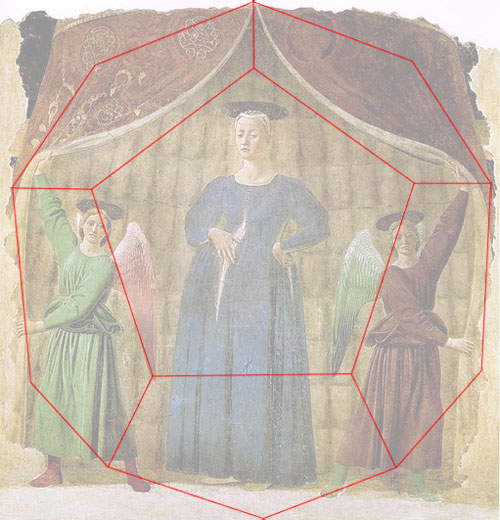Piero della Francesca, Madonna del Parto (vers 1455 ; Monterchi, Museo della Madonna del Parto) dans l’espace marqué par un dodécaèdre. Dans cette image comme dans la suivante, nous avons éclairci les couleurs des peintures pour mieux faire ressortir les formes géométriques.

Piero della Francesca, Flagellation (vers 1460 ; Urbino, Galleria Nazionale delle Marche) avec les lignes de perspective mises en évidence, le point de fuite (le point rouge) et les lignes du cube dans lequel se déroule la scène de gauche.

Avertissement : la traduction en français de l'article original italien a été réalisée à l'aide d'outils automatiques. Nous nous engageons à réviser tous les articles, mais nous ne garantissons pas l'absence totale d'inexactitudes dans la traduction dues au programme. Vous pouvez trouver l'original en cliquant sur le bouton ITA. Si vous trouvez une erreur,veuillez nous contacter.