Piero della Francesca y la importancia de su tratado "De quinque corporibus regularibus".

Es bien sabido que Piero della Francesca no sólo fue un artista excepcional, sino también un consumado tratadista. Cualquiera que haya estudiado un mínimo de historia del arte renacentista sabe desde siempre que el gran artista toscano escribió cuatro tratados, entre ellos el fundamental De prospectiva pingendi, dedicado a la perspectiva científica. Tan fundamental que, al hablar de los tratados de Piero, se corre el riesgo de despreciar los demás, y en particular el De quinque corporibus regolaribus, de no menor importancia que el más famoso de los escritos de Piero. Y, en efecto, muy pocos libros de historia del arte proporcionan información en profundidad sobre este tratado: la mayoría de las veces, se limitan a señalar que se trata de un libro sobre los cinco sólidos regulares, y luego pasan a otra cosa.

Sin embargo, surge espontáneamente una pregunta: ¿por qué iba Piero della Francesca a dedicar todo un tratado a un tema tan técnico y específico como los cinco sólidos regulares? Partamos de una premisa. Como es bien sabido, Piero della Francesca fue uno de los artistas más atraídos por las leyes matemáticas y geométricas que regulan el espacio, ya que él (al igual que otros artistas) las consideraba fundamentales para resolver una de las cuestiones más antiguas de la pintura: la representación de un espacio tridimensional sobre un soporte bidimensional. Por esta razón, según Piero della Francesca, todo estudio relativo a la geometría está dotado de una finalidad práctica de gran importancia: poder reproducir el espacio de la realidad sobre una pared o un panel (Piero nunca trabajó sobre lienzo). Sin embargo, antes de seguir adelante, veamos más de cerca de qué trata el De quinque corporibus regularibus.

Dos folios del De quinque corporibus regularibus (Manuscrito cod. Urb. lat. 632 fol. 40 verso - 41 recto; Roma, Ciudad del Vaticano, Biblioteca Vaticana. El manuscrito es de autor desconocido, las correcciones y notas son de Piero della Francesca)

Hemos dicho que el tratado, escrito en latín, está enteramente dedicado a los cinco sólidos regulares. Estos últimos no son más que poliedros, es decir, sólidos cuya superficie está formada por caras poligonales que, frente a todos los demás poliedros, tienen la característica de tener todas sus caras, aristas y ángulos iguales, de igual tamaño. El descubrimiento de los sólidos regulares se atribuye a Pitágoras, pero el primero en hablar de ellos es Platón en su Timeo: Platón fue el primero en describirlos con detalle, aunque el primero en describir cómo se construyen será, unas décadas más tarde, Euclides (y de hecho Piero se inspiró en Euclides). Pero Platón no se limitó a describirlos, pues también se preocupó de dar a los sólidos regulares un valor simbólico: así, cuatro de ellos se asociaron a los cuatro elementos del universo, y uno (el dodecaedro) fue símbolo del universo mismo. A Piero no le interesaba todo esto: Piero della Francesca estudió los cinco poliedros regulares con fines puramente prácticos. Pero, ¿cuáles son los cinco poliedros regulares? Aquí están: la pirámide de base triangular, es decir, el tetraedro (cuatro caras triangulares, obviamente se trata de triángulos equiláteros), el cubo también llamado hexaedro (seis caras cuadradas), eloctaedro (ocho caras triangulares), el dodecaedro (doce caras pentagonales) y el icosaedro (veinte caras triangulares). No son posibles otros sólidos regulares, es decir, no es posible encontrar otras combinaciones que den como resultado un poliedro que tenga todas las caras de igual superficie (y sobre todo que sean polígonos regulares), todas las aristas de igual tamaño y todos los ángulos de la misma abertura.

Uno de los mejores amigos de Piero della Francesca, el matemático Luca Pacioli, desarrolló lo que el pintor había escrito en su tratado De divina proportione, e hizo que Leonardo da Vinci ilustrara su tratado. Así es como Leonardo representó los poliedros regulares:

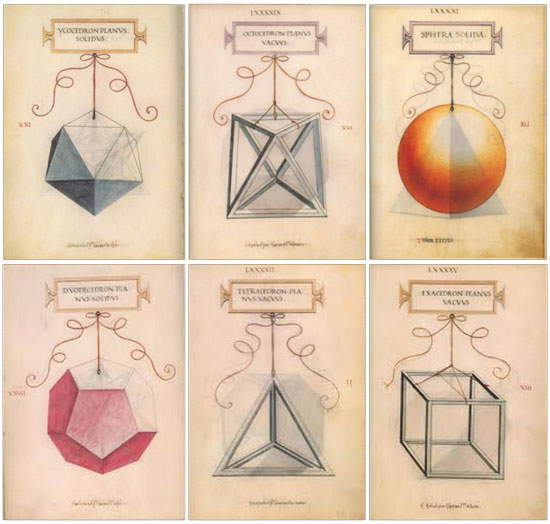Los cinco poliedros regulares (junto con la esfera, en la que todos pueden inscribirse) dibujados por Leonardo da Vinci para el De divina proportion e de Luca Pacioli en 1509. Arriba, de izquierda a derecha: icosaedro, octaedro, esfera. Abajo, desde la izquierda: dodecaedro, tetraedro, cubo o hexaedro.

Pero vayamos a la importancia de la obra, y a por qué la escribió Piero della Francesca. El artista era consciente de que existía una profunda conexión entre los cinco cuerpos regulares y la perspectiva, la técnica que, como ya se ha dicho, permite representar el espacio tridimensional sobre un soporte bidimensional. Practicar los sólidos regulares significaba al mismo tiempo aprender el dibujo en perspectiva, fundamental para una representación del espacio sobre una base científica: y de hecho, el libro está lleno de ejercicios matemáticos y geométricos, algunos de ellos bastante abstractos, que ayudan al artista que lo lee a practicar el dibujo, a aprender sobre el espacio. Representar un espacio tridimensional, para Piero, presupone estudiar analíticamente los objetos que lo componen, en sus formas, en su posición respecto al lugar que los contiene, en su relación con otros objetos. El estudio de los poliedros regulares no es sino una forma de abordar lo que más tarde será el estudio de formas más complejas (como la figura humana, probablemente la más complicada de representar en perspectiva).

El hecho de que exista un vínculo entre el dibujo en perspectiva y el dibujo de sólidos geométricos nos lo revela también un detalle ajeno al tratado en sí, pero no por ello menos significativo: el opúsculo De quinque corporibus regularibus que, no hemos mencionado aún, fue escrito entre 1482 y 1492, está dedicado al tercer duque de Urbino, Guidobaldo da Montefeltro. El anterior De prospectiva pingendi, que fue compuesto aproximadamente entre 1472 y 1475, fue dedicado en cambio al padre de Guidobaldo, Federico da Montefeltro: hay, en suma, una continuidad entre el tratado más antiguo y el más reciente, por lo tanto hay una continuidad entre los temas abordados, y esta continuidad está bien ejemplificada por las dedicatorias. Pero no sólo: es el propio Piero, en la dedicatoria, quien relaciona el De quinque corporibus regularibus con el De prospectiva. Leemos, en efecto, estas palabras: “Nec dedignabitur celsitudo tua ex hoc iam emerito, et fere vetustate consumpto agello, unde et illustrissimus genitor tuus, uberiores percepit, hos exiles et inanes fructus suscipere, et libellum ipsum inter innumera amplissimae tuae, paternaeque bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, prò pedissequo et aliorum servulo, vel in angulo collocare”. Que se traducen más o menos así: “Vuestra Alteza no desdeñará aceptar, de este campo ahora consumido por la vejez, y del que vuestro ilustre progenitor cosechó ya frutos más ricos, este magro y vano producto, ni desdeñará colocar este opúsculo, entre los innumerables volúmenes de vuestra vasta biblioteca paterna, en un rincón junto a mi opúsculo sobre la Perspectiva, que escribí en años pasados como un fiel pequeño servidor”.

Sección IV (“Los cuerpos geométricos”) de la exposición Piero della Francesca. Il disegno tra arte e scienza, Reggio Emilia, Palazzo Magnani, 14 de marzo - 14 de junio de 2015. ¡La foto es de Mostre-rò, a quien agradecemos su amable permiso!

En la dedicatoria del libro sobre sólidos regulares también se esboza brevemente el contenido del tratado. De hecho, el trabajo consta de cuatro partes: la primera contiene problemas de geometría plana, que son importantes porque sin nociones de geometría plana no se puede estudiar la geometría de los sólidos. Esta última se trata en las partes siguientes: la segunda introduce los poliedros regulares y propone ejercicios sobre este tema, la tercera trata de los poliedros inscritos en otros poliedros y, finalmente, la última parte está dedicada a los poliedros irregulares. Cada ejercicio va acompañado de dibujos explicativos: una práctica que hoy nos parece obvia, pero que no lo era en aquella época. Por ejemplo, Leon Battista Alberti, que expuso varios principios de la geometría euclidiana en su De pictura(Euclides fue un importante punto de referencia tanto para Alberti como para Piero), no añadió ningún dibujo, ya que estaba muy extendida entre los intelectuales humanistas de la época la creencia de que las palabras bastaban por sí solas para explicar un concepto. Piero della Francesca, en cambio, como persona pragmática y concreta que era, se dio cuenta de que para transmitir mejor los conceptos era necesario ayudarse de dibujos, que nunca faltaron en sus tratados.

Concluyamos diciendo que, para Piero, los sólidos regulares no eran sólo objetos sobre los que practicar. A menudo, el pintor utilizaba poliedros regulares para construir el espacio en el que ambientaba sus cuadros. Así pues, hemos analizado dos de sus obras célebres, la Madonna del Parto y la Flagelación, para buscar estructuras espaciales derivadas de los sólidos regulares. Así, podemos ver cómo la Madonna del Parto fue creada a partir de un dodecaedro, mientras que el escenario en el que Jesús sufre la flagelación en el famoso cuadro de Urbino no es más que un cubo abierto estudiado en perspectiva. Pero estamos convencidos de que el mismo tipo de investigación puede hacerse en otros cuadros de Piero... ¡!

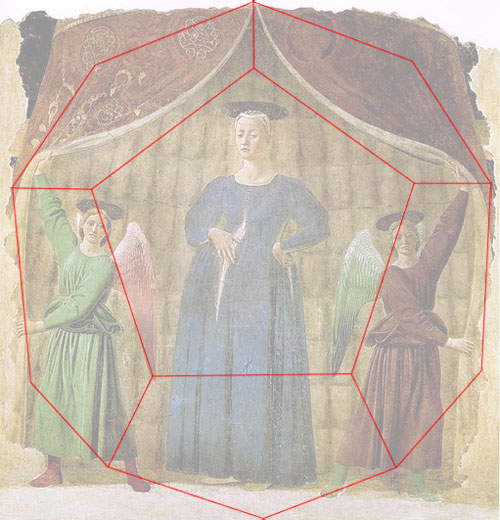Piero della Francesca, Madonna del Parto (c. 1455; Monterchi, Museo della Madonna del Parto) en el espacio marcado por un dodecaedro. Tanto en esta imagen como en la siguiente, hemos aclarado los colores de las pinturas para hacer más evidentes las formas geométricas.

Piero della Francesca, Flagelación (c. 1460; Urbino, Galleria Nazionale delle Marche) con las líneas de perspectiva resaltadas, el punto de fuga (el punto rojo) y las líneas del cubo dentro del cual se desarrolla la escena de la izquierda.

Advertencia: la traducción al español del artículo original en italiano se ha realizado mediante herramientas automáticas. Nos comprometemos a revisar todos los artículos, pero no garantizamos la ausencia total de imprecisiones en la traducción debidas al programa. Puede encontrar el original haciendo clic en el botón ITA. Si encuentra algún error, por favor contáctenos.