Piero della Francesca and the importance of his treatise De quinque corporibus regularibus

It is well known that Piero della Francesca was not only an outstanding artist but also a highly accomplished treatise writer. Anyone who has studied even a modicum of Renaissance art history has always known that the great Tuscan artist wrote four treatises, including the fundamental De prospectiva pingendi, devoted to scientific perspective. So fundamental, that when people talk about Piero’s treatises, they run the risk of snubbing the others, and in particular the De quinque corporibus regolaribus, of no less importance than the most famous Pierfrancesque writing. And indeed, few art history books provide in-depth information on this treatise: we are limited, most often, to pointing out that it is a book on the five regular solids, and then move on.

However, one question arises: why would Piero della Francesca have devoted an entire treatise to such a technical and specific topic as the five regular solids? Let us start with a premise. As is well known, Piero della Francesca was one of the artists most attracted to the mathematical and geometric laws that govern space, since they were considered by him (as by other artists) to be fundamental in solving one of the most long-standing issues in painting: the representation of a three-dimensional space on a two-dimensional support. For this reason, according to Piero della Francesca, every study involving geometry comes with a practical purpose of high importance: being able to reproduce the space of reality on a wall or a panel (Piero never worked on canvas). Before we go any further, however, let us take a closer look at what the De quinque corporibus regularibus is about.

Two folios of the De quinque corporibus regularibus (Manuscript cod. Urb. lat. 632 fol. 40 verso - 41 recto; Rome, Vatican City, Biblioteca Apostolica Vaticana. The manuscript is by an unknown author; the corrections and notes are by Piero della Francesca)

We said that the treatise, written in Latin, is entirely devoted to the five regular solids. The latter are nothing but polyhedra, that is, solids whose surface is formed by polygonal faces, which in comparison with all other polyhedra have the characteristic of having all faces, edges and angles equal, of equal size. The discovery of regular solids is attributed to Pythagoras, but the first to mention them is Plato in his Timaeus.Plato was the first to describe them in detail, although the first to describe how they are constructed will be, a few decades later, Euclid (and in fact, Piero was inspired by Euclid himself). However, Plato did more than just describe them, for he was also concerned to give the regular solids a symbolic value: four of them were thus associated with the four elements of the universe, and one (the dodecahedron) was symbolic of the universe itself. Piero was not interested in all this: Piero della Francesca studied the five regular polyhedra for purely practical purposes. But what are the five regular polyhedra? Here they are: the pyramid with a triangular base, that is, the tetrahedron (four triangular faces, of course we are talking about equilateral triangles), the cube also called the hexahedron (six square faces), theoctahedron (eight triangular faces), the dodecahedron (twelve pentagonal faces) and theicosahedron (twenty triangular faces). No other regular solids are possible, that is, no other combinations can be found that result in a polyhedron that has all faces of equal surface area (and more importantly, are regular polygons), all edges of equal size, and all angles of the same opening.

One of Piero della Francesca’s best friends, mathematician Luca Pacioli, developed in his treatise De divina proportione what the painter had written, and had his treatise illustrated by Leonardo da Vinci. This is how Leonardo depicted regular polyhedra:

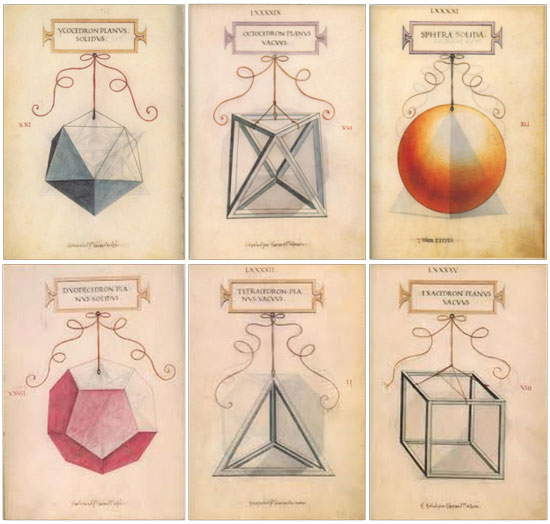The five regular polyhedra (along with the sphere, in which they can all be inscribed) drawn by Leonardo da Vinci for Luca Pacioli’s De divina proportione in 1509. Top, from left: icosahedron, octahedron, sphere. Bottom, from left: dodecahedron, tetrahedron, cube or hexahedron.

But let us come to the importance of the work, and why Piero della Francesca wrote it. The artist was aware that there was a profound connection between the five regular bodies and perspective, the technique that, as mentioned above, allows the depiction of three-dimensional space on a two-dimensional support. Practicing on the regular solids meant meanwhile learning perspective drawing, which is fundamental for a scientifically based representation of space: and in fact, the book is full of mathematical and geometrical exercises, some of them even quite abstract, that help the artist reading it to practice drawing, to learn about space. Representing a three-dimensional space, for Piero, presupposes that the objects that compose it are studied analytically, in their shapes, in their position in relation to the place that contains them, in their relationship to other objects. The study of regular polyhedra is but one way to approach what will be, later, the study of more complex forms (such as the human figure, probably the most complicated to represent in perspective).

That there is a link between perspective drawing and the drawing of geometric solids is also revealed to us by a detail unrelated to the treatment itself, but nonetheless significant: the booklet De quinque corporibus regularibus which, we have not yet mentioned, was written between 1482 and 1492, is dedicated to the third Duke of Urbino, Guidobaldo da Montefeltro. The earlier De prospectiva pingendi, composed roughly between 1472 and 1475, on the other hand, was dedicated to Guidobaldo’s father, Federico da Montefeltro: there is, in short, a continuity between the older treatise and the newer one, so there is a continuity between the topics addressed, and this continuity is well exemplified by the dedications. But not only that: it is Piero himself, in the dedication, who relates the De quinque corporibus regularibus to the De prospectiva. We read, in fact, these words: “Nec dedignabitur celsitudo tua ex hoc iam emerito, et fere vetustate consumpto agello, unde et illustrissimus genitor tuus, uberiores percepit, hos exiles et inanes fructus suscipere, et libellum ipsum inter innumera amplissimae tuae, paternaeque bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, prò pedissequo et aliorum servulo, vel in angulo collocare.” Which translated sound more or less like this: “Your Highness will not disdain to accept, from this little field now consumed by old age, and from which Your most illustrious parent already reaped richer fruits, this meager and vain product, nor will He disdain to place this little book, among the innumerable volumes of Your most vast paternal library, in a corner next to my pamphlet on Perspective, which I wrote in past years as a faithful little servant.”

Section IV (“Geometric Bodies”) of the exhibition Piero della Francesca. Drawing between Art and Science, Reggio Emilia, Palazzo Magnani, March 14-June 14, 2015. The photo is by Mostre-rò whom we thank for the kind permission!

In the dedication of the book on regular solids, the contents of the treatise are also briefly laid out. In fact, the paper consists of four parts: the first contains problems in plane geometry, which are important because without notions of plane geometry one cannot study the geometry of solids. The latter is dealt with in the following parts: the second introduces regular polyhedra and offers exercises on this topic, in the third we discuss polyhedra inscribed in other polyhedra, and finally the last part is devoted to irregular polyhedra. Each exercise is accompanied by explanatory drawings-a practice that seems obvious to us today, but in those days it was not so. For example, Leon Battista Alberti, who expounded several principles of Euclidean geometry in his De pictura(Eu clid was an important point of reference for both Alberti and Piero), had not added any drawings, since there was a widespread belief among the humanist intellectuals of the time that words alone were sufficient to explain a concept. Piero della Francesca, on the other hand, being the pragmatic and concrete individual that he was, realized that in order to get concepts across better it was necessary to help himself with drawings, which are never lacking in his treatises.

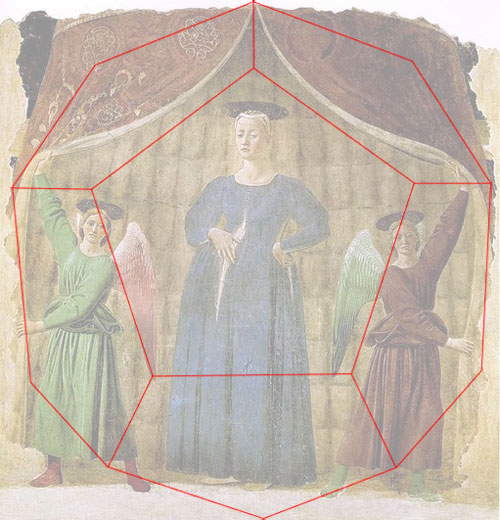
Let us conclude by saying that for Piero, regular solids were not just objects to practice on. Often, the painter used regular polyhedra to construct the space within which he set his paintings. We therefore analyzed two of his famous works, the Madonna del Parto and the Flagellation, to look for spatial structures derived from regular solids. Thus we can see that the Madonna del Par to was made from a dodecahedron, while the setting in which Jesus undergoes the flagellation in the famous Urbino painting is nothing more than an open cube studied in perspective. But we are convinced that the same kind of investigation can be done in other paintings by Piero as well.... !

Piero della Francesca, Madonna del Par to (c. 1455; Monterchi, Museum of the Madonna del Parto) in the space marked by a dodecahedron. In both this image and the next, we have lightened the colors of the paintings to make the geometric shapes more obvious.

Piero della Francesca, Flagellation (c. 1460; Urbino, Galleria Nazionale delle Marche) with highlighted perspective lines, vanishing point (the red dot) and the lines of the cube within which the scene on the left is set.

Warning: the translation into English of the original Italian article was created using automatic tools. We undertake to review all articles, but we do not guarantee the total absence of inaccuracies in the translation due to the program. You can find the original by clicking on the ITA button. If you find any mistake,please contact us.