Piero della Francesca und die Bedeutung seiner Abhandlung "De quinque corporibus regularibus".

Es ist bekannt, dass Piero della Francesca nicht nur ein außergewöhnlicher Künstler war, sondern auch ein äußerst fähiger Traktatschreiber. Jeder, der auch nur ein Minimum an Kunstgeschichte der Renaissance studiert hat, weiß, dass der große toskanische Künstler vier Traktate geschrieben hat, darunter das grundlegende De prospectiva pingendi, das der wissenschaftlichen Perspektive gewidmet ist. So grundlegend, dass man, wenn man von Pieros Traktaten spricht, Gefahr läuft, die anderen zu vernachlässigen, insbesondere das De quinque corporibus regolaribus, das nicht weniger wichtig ist als die berühmteste der Schriften Pieros. Und in der Tat gibt es nur wenige kunsthistorische Bücher, die sich mit diesem Traktat eingehend befassen: Meistens wird nur darauf hingewiesen, dass es sich um ein Buch über die fünf regelmäßigen Körper handelt, und dann geht es weiter.

Eine Frage stellt sich jedoch spontan: Warum sollte Piero della Francesca einem so technischen und spezifischen Thema wie den fünf regelmäßigen Körpern eine ganze Abhandlung widmen? Beginnen wir mit einer Vorbemerkung. Bekanntlich war Piero della Francesca einer der Künstler, die sich am meisten für die mathematischen und geometrischen Gesetze, die den Raum regeln, interessierten, da er (wie auch andere Künstler) sie als grundlegend für die Lösung eines der ältesten Probleme der Malerei betrachtete: die Darstellung eines dreidimensionalen Raums auf einem zweidimensionalen Träger. Aus diesem Grund hat für Piero della Francesca jede geometrische Studie einen sehr wichtigen praktischen Zweck: den Raum der Realität auf einer Wand oder einer Tafel wiederzugeben (Piero hat nie auf Leinwand gearbeitet). Bevor wir jedoch weitergehen, sollten wir uns genauer ansehen, worum es in De quinque corporibus regularibus geht.

Zwei Blätter des De quinque corporibus regular ibus (Manuskript cod. Urb. lat. 632 fol. 40 verso - 41 recto; Rom, Vatikanstadt, Vatikanische Bibliothek. Das Manuskript stammt von einem unbekannten Autor, die Korrekturen und Anmerkungen stammen von Piero della Francesca)

Wir haben gesagt, dass die in Latein verfasste Abhandlung ganz den fünf regelmäßigen Körpern gewidmet ist. Letztere sind nichts anderes als Polyeder, d.h. Körper, deren Oberfläche von polygonalen Flächen gebildet wird, die im Vergleich zu allen anderen Polyedern die Eigenschaft haben, dass alle ihre Flächen, Kanten und Winkel gleich groß sind. Die Entdeckung regelmäßiger Körper wird Pythagoras zugeschrieben, aber der erste, der von ihnen spricht, ist Platon in seinem Timaios: Platon war der erste, der sie detailliert beschrieb, obwohl der erste, der ihre Konstruktion beschrieb, einige Jahrzehnte später Euklid sein wird (und in der Tat wurde Piero von Euklid inspiriert). Platon beschränkte sich jedoch nicht darauf, sie zu beschreiben, sondern gab den regelmäßigen Körpern auch einen symbolischen Wert: Vier von ihnen wurden mit den vier Elementen des Universums in Verbindung gebracht, und einer (das Dodekaeder) war ein Symbol für das Universum selbst. Piero war an all dem nicht interessiert: Piero della Francesca studierte die fünf regelmäßigen Polyeder aus rein praktischen Gründen. Aber was sind die fünf regelmäßigen Polyeder? Es handelt sich um die Pyramide mit dreieckiger Grundfläche, d. h. das Tetraeder (vier dreieckige Flächen, es handelt sich also um gleichseitige Dreiecke), den Würfel, auch Hexaeder genannt (sechs quadratische Flächen), dasOktaeder (acht dreieckige Flächen), das Dodekaeder (zwölf fünfeckige Flächen) und dasIkosaeder (zwanzig dreieckige Flächen). Andere regelmäßige Körper sind nicht möglich, d. h. es ist nicht möglich, andere Kombinationen zu finden, die ein Polyeder ergeben, bei dem alle Flächen gleich groß sind (und vor allem regelmäßige Vielecke sind), alle Kanten gleich groß und alle Winkel gleich offen sind.

Einer der besten Freunde von Piero della Francesca, der Mathematiker Luca Pacioli, entwickelte das, was der Maler in seinem Traktat De divina proportione geschrieben hatte, weiter und ließ sein Traktat von Leonardo da Vinci illustrieren. Auf diese Weise stellte Leonardo regelmäßige Polyeder dar:

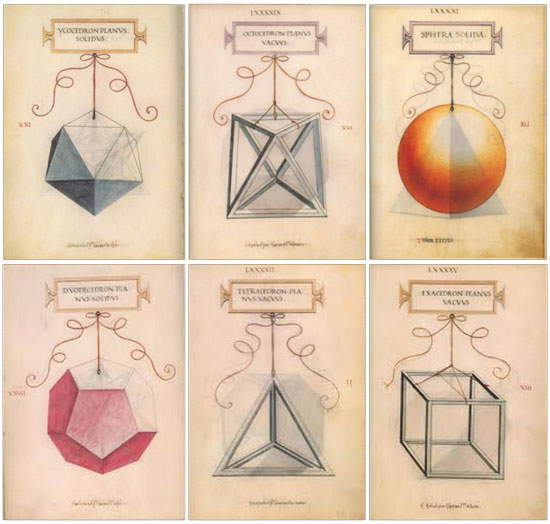Die fünf regelmäßigen Polyeder (zusammen mit der Kugel, in die sie alle eingeschrieben werden können), gezeichnet von Leonardo da Vinci für Luca Paciolis De divina proportione im Jahr 1509. Oben, von links: Ikosaeder, Oktaeder, Kugel. Unten, von links: Dodekaeder, Tetraeder, Würfel oder Hexaeder.

Doch kommen wir nun zur Bedeutung des Werks und zu den Gründen, warum Piero della Francesca es geschrieben hat. Der Künstler war sich bewusst, dass zwischen den fünf regelmäßigen Körpern und der Perspektive, der Technik, die, wie bereits erwähnt, die Darstellung des dreidimensionalen Raums auf einem zweidimensionalen Untergrund ermöglicht, ein tiefer Zusammenhang besteht. Das Üben der regelmäßigen Körper bedeutete gleichzeitig das Erlernen des perspektivischen Zeichnens, das für die Darstellung des Raums auf wissenschaftlicher Grundlage von grundlegender Bedeutung ist: und tatsächlich ist das Buch voll von mathematischen und geometrischen Übungen, von denen einige recht abstrakt sind, die dem Künstler, der es liest, helfen, das Zeichnen zu üben und den Raum zu verstehen. Die Darstellung eines dreidimensionalen Raums setzt für Piero voraus, dass die Objekte, aus denen er sich zusammensetzt, analytisch untersucht werden, und zwar in ihren Formen, in ihrer Position in Bezug auf den Raum, in dem sie sich befinden, und in ihrer Beziehung zu anderen Objekten. Das Studium regelmäßiger Polyeder ist nur eine Möglichkeit, sich dem zu nähern, was später das Studium komplexerer Formen sein wird (wie die menschliche Figur, die wahrscheinlich am kompliziertesten in der Perspektive darzustellen ist).

Dass es eine Verbindung zwischen dem perspektivischen Zeichnen und dem Zeichnen geometrischer Körper gibt, zeigt uns auch ein Detail, das nichts mit der eigentlichen Abhandlung zu tun hat, aber dennoch von Bedeutung ist: Das Büchlein De quinque corporibus regularibus, das wir noch nicht erwähnt haben, wurde zwischen 1482 und 1492 geschrieben und ist dem dritten Herzog von Urbino, Guidobaldo da Montefeltro, gewidmet. Das vorangegangene De prospectiva pingendi, das etwa zwischen 1472 und 1475 entstand, wurde hingegen Guidobaldos Vater, Federico da Montefeltro, gewidmet: Es besteht also eine Kontinuität zwischen dem älteren und dem jüngeren Werk, und damit auch eine Kontinuität zwischen den behandelten Themen, die sich in den Widmungen gut widerspiegelt. Aber nicht nur: es ist Piero selbst, der in der Widmung das De quinque corporibus regularibus mit dem De prospectiva in Beziehung setzt. Wir lesen in der Tat diese Worte: “Nec dedignabitur celsitudo tua ex hoc iam emerito, et fere vetustate consumpto agello, unde et illustrissimus genitor tuus, uberiores percepit, hos exiles et inanes fructus suscipere, et libellum ipsum inter innumera amplissimae tuae, paternaeque bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, prò pedissequo et aliorum servulo, vel in angulo collocare”. Die Übersetzung lautet in etwa so: “Eure Hoheit wird nicht verschmähen, von dem Feld, das das Alter nun verzehrt und von dem Eure erlauchten Eltern schon reichere Früchte geerntet haben, dieses magere und eitle Produkt anzunehmen, noch wird er verschmähen, dieses Büchlein unter den unzähligen Bänden Eurer großen väterlichen Bibliothek in eine Ecke neben meine Broschüre über die Perspektive zu stellen, die ich in den vergangenen Jahren als treuer kleiner Diener geschrieben habe”.

Abschnitt IV (“Die geometrischen Körper”) der Ausstellung Piero della Francesca. Il disegno tra arte e scienza, Reggio Emilia, Palazzo Magnani, 14. März - 14. Juni 2015. Das Foto stammt von Mostre-rò, dem wir für seine freundliche Genehmigung danken!

In der Widmung des Buches über regelmäßige Festkörper wird auch der Inhalt der Abhandlung kurz umrissen. Die Arbeit besteht eigentlich aus vier Teilen: Der erste enthält Probleme der ebenen Geometrie, die wichtig sind, weil man ohne Begriffe der ebenen Geometrie die Geometrie der Körper nicht studieren kann. Letztere wird in den folgenden Teilen behandelt: Der zweite Teil führt in regelmäßige Polyeder ein und bietet Übungen zu diesem Thema an, der dritte Teil befasst sich mit Polyedern, die in andere Polyeder eingeschrieben sind, und der letzte Teil schließlich ist den unregelmäßigen Polyedern gewidmet. Jede Übung wird von erklärenden Zeichnungen begleitet: eine Praxis, die uns heute selbstverständlich erscheint, es aber damals nicht war. Leon Battista Alberti zum Beispiel, der in seinem Werk De pictura mehrere Prinzipien der euklidischen Geometrie darlegte(Euklid war sowohl für Alberti als auch für Piero ein wichtiger Bezugspunkt), fügte keine Zeichnungen hinzu, da unter den humanistischen Intellektuellen jener Zeit die Überzeugung weit verbreitet war, dass Worte allein ausreichen, um ein Konzept zu erklären. Piero della Francesca hingegen, der ein pragmatischer und konkreter Mensch war, erkannte, dass es zur besseren Vermittlung von Konzepten notwendig war, mit Zeichnungen nachzuhelfen, die in seinen Abhandlungen nie fehlten.

Abschließend lässt sich sagen, dass für Piero die regelmäßigen Körper nicht nur Übungsobjekte waren. Oft benutzte der Maler regelmäßige Polyeder, um den Raum zu konstruieren, in den er seine Bilder stellte. Wir haben daher zwei seiner berühmten Werke, die Madonna del Parto und die Geißelung, analysiert, um nach räumlichen Strukturen zu suchen, die von regelmäßigen Körpern abgeleitet sind. So können wir sehen, wie die Madonna del Parto aus einem Dodekaeder entstanden ist, während die Umgebung, in der Jesus in dem berühmten Gemälde aus Urbino gegeißelt wird, nichts anderes als ein perspektivisch betrachteter offener Würfel ist. Aber wir sind überzeugt, dass die gleiche Art von Untersuchung auch bei anderen Gemälden von Piero durchgeführt werden kann... !

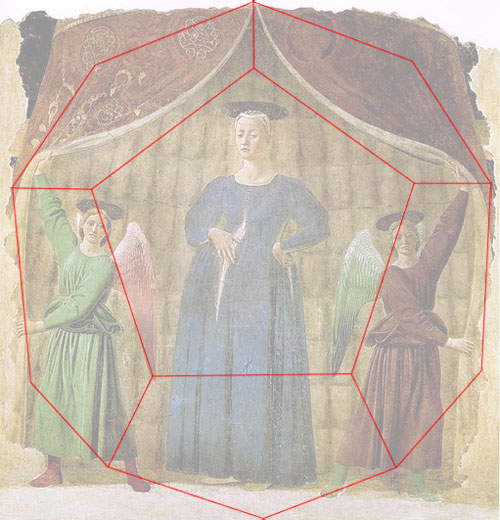Piero della Francesca, Madonna del Parto (um 1455; Monterchi, Museo della Madonna del Parto) in dem von einem Dodekaeder markierten Raum. Sowohl auf diesem als auch auf dem nächsten Bild haben wir die Farben der Gemälde aufgehellt, um die geometrischen Formen deutlicher hervorzuheben.

Piero della Francesca, Geißelung (um 1460; Urbino, Galleria Nazionale delle Marche) mit hervorgehobenen perspektivischen Linien, dem Fluchtpunkt (roter Punkt) und den Linien des Würfels, in dem sich die Szene links befindet.

Achtung: Die Übersetzung des italienischen Originalartikels ins Deutsche wurde mit Hilfe automatischer Tools erstellt. Wir verpflichten uns, alle Artikel zu überprüfen, aber wir garantieren nicht die völlige Abwesenheit von Ungenauigkeiten in der Übersetzung aufgrund des Programms. Sie können das Original finden, indem Sie auf die ITA-Schaltfläche klicken. Wenn Sie einen Fehler finden, kontaktieren Sie uns bitte.